Opposite of deterministic

Science and life // Illustrations

Trees, like many other objects in nature, have a fractal structure.

Science and life // Illustrations

Crimean pine (left) and artificial fractal structure (right) are surprisingly similar.

Response of an oscillatory circuit to an external periodic signal: a - periodic response of a linear circuit, b - chaotic response of a nonlinear circuit. The role of the non-linear capacitance is performed by the p-n junction of the semiconductor diode. nine0005

The motion of a dynamical system can be visualized by a trajectory on the phase plane, where the X and Y axes are the generalized coordinate and momentum of the particle. a - oscillations of a damped pendulum.

Examples of systems with chaos.

Science and life // Illustrations

The main ways of synchronization of chaotic systems: a - through global connections: each system influences each; b - with the help of a pacemaker, or "pacemaker": one of the systems sets the rhythm for all other elements. nine0005

Science and life // Illustrations

An example of recording information using deterministic chaos.

Employees of the InformChaos laboratory of the Institute of Radio Engineering and Electronics of the Russian Academy of Sciences AI Panas and SO Starkov conduct an experiment on high-speed direct chaotic data transmission in the microwave range (above).

This is what chaotic microwave oscillations look like, which make it possible to increase the information transfer rate tenfold compared to traditional systems.

‹

›

View full size

What is a fractal?

Fractals are everywhere around us, both in the outlines of mountains and in the winding line of the sea coast. Some of the fractals are constantly changing, like moving clouds or flickering flames, while others, like trees or our vascular systems, retain an evolutionary structure.
H. O. Peigen and P. H. Richter.

The geometry that we studied in school and that we use in everyday life goes back to Euclid (about 300 BC). Triangles, squares, circles, parallelograms, parallelepipeds, pyramids, balls, prisms are typical objects considered by classical geometry. Man-made objects usually include these figures or their fragments. However, in nature they are not so common. Indeed, do forest beauties, for example, look like any of the listed items or a combination of them? It is easy to see that, unlike the forms of Euclid, natural objects do not have smoothness, their edges are broken, jagged, surfaces are rough, corroded by cracks, passages and holes.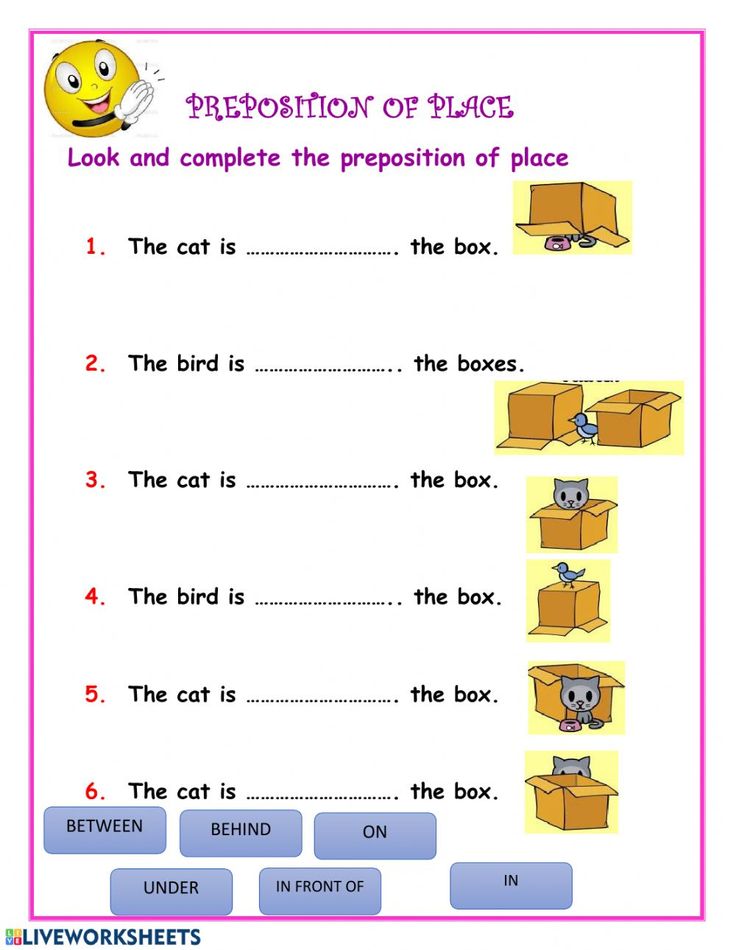 "Why is geometry often called cold and dry? One reason is its inability to describe the shape of a cloud, a mountain, a tree, or a seashore. Clouds are not spheres, mountains are not cones, coastlines are not circles, and the crust is not smooth." , and lightning does not travel in a straight line. Nature shows us not just a higher degree, but a completely different level of complexity," - with these words begins "The Fractal Geometry of Nature", written by Benoit Mandelbrot. It was him at 19In 75, he first introduced the concept of a fractal - from the Latin word fractus, a broken stone, split and irregular. It turns out that almost all natural formations have a fractal structure. What does it mean? If you look at a fractal object as a whole, then at its part on an enlarged scale, then at a part of this part, etc., it is easy to see that they look the same. Fractals are self-similar - their shape is reproduced on different scales.

The discovery of fractals revolutionized not only geometry, but also physics, chemistry, and biology. Fractal algorithms have also found application in information technologies, for example, for the synthesis of three-dimensional computer images of natural landscapes, for data compression (compression) (see "Science and Life" No. 4, 1994; Nos. 8, 12, 1995; No. 7, 1998). Further, we will see that the concept of a fractal is closely related to another no less curious phenomenon - chaos in dynamical systems.

Determinism and chaos

CHAOS (Greek caos) - in Greek mythology boundless primitive mass,
from which
was subsequently formed everything that exists. In a figurative sense - a mess, confusion.
Encyclopedia
Cyril and Methodius

When they talk about the determinism of a certain system, they mean that its behavior is characterized by an unambiguous causal relationship. That is, knowing the initial conditions and the law of motion of the system, it is possible to accurately predict its future. It is this idea of ​​motion in the Universe that is characteristic of classical, Newtonian dynamics. Chaos, on the contrary, implies a chaotic, random process, when the course of events can neither be predicted nor reproduced. What is a deterministic chaos - a seemingly impossible union of two opposite concepts? nine0005

Let's start with a simple experience. A ball suspended on a thread is deflected from the vertical and released. There are fluctuations. If the ball is deflected slightly, then its motion is described by linear equations. If the deviation is made large enough, the equations will no longer be linear. What will change with this? In the first case, the oscillation frequency (and, accordingly, the period) does not depend on the degree of the initial deviation. In the second - such dependence takes place. A complete analog of a mechanical pendulum as an oscillatory system is an oscillatory circuit, or "electric pendulum". In the simplest case, it consists of an inductor, a capacitor (capacitance) and a resistor (resistance). If all three of these elements are linear, then the oscillations in the circuit are equivalent to oscillations of a linear pendulum. But if, for example, the capacitance is non-linear, the oscillation period will depend on their amplitude. nine0005

The dynamics of an oscillatory circuit is determined by two variables, for example, the current in the circuit and the voltage across the capacitance. If these quantities are plotted along the X and Y axes, then each state of the system will correspond to a certain point on the resulting coordinate plane. Such a plane is called phase . (Accordingly, if a dynamic system is determined by n variables, then instead of a two-dimensional phase plane, it can be assigned n- dimensional phase space .)

Now let's start acting on our pendulums with an external periodic signal. The response of linear and non-linear systems will be different. In the first case, regular periodic oscillations will gradually be established with the same frequency as the frequency of the driving signal. On the phase plane, this movement corresponds to a closed curve, called attractor (from the English verb to attract - attract), - a set of trajectories that characterize the steady process. In the case of a nonlinear pendulum, complex, non-periodic oscillations can arise when the trajectory on the phase plane does not close in an arbitrarily long time. In this case, the behavior of a deterministic system will outwardly resemble a completely random process - this is the phenomenon dynamic or deterministic chaos . The image of chaos in the phase space - chaotic attractor - has a very complex structure: it is a fractal. Because of its unusual properties, it is also called the strange attractor .

Why does a system that develops according to well-defined laws behave chaotically? The influence of extraneous noise sources, as well as quantum probability, has nothing to do with it in this case. Chaos is generated by the intrinsic dynamics of a nonlinear system - its property to exponentially quickly separate arbitrarily close trajectories. As a result, the shape of the trajectories depends very strongly on the initial conditions. Let us explain what this means by the example of a nonlinear oscillatory circuit under the influence of an external periodic signal. We introduce a small perturbation into our system - we change the initial charge of the capacitor a little. Then the oscillations in the perturbed and unperturbed circuits, initially practically synchronous, will very soon become completely different. Since in a real physical experiment it is possible to set the initial conditions only with finite accuracy, it is impossible to predict the behavior of chaotic systems for a long time. nine0005

Predicting the future

- Because of such smallness! Because of the butterfly! Eckels shouted.
She fell to the floor, a graceful little creature capable of breaking the balance, little dominoes fell... big dominoes... huge dominoes, connected by a chain of innumerable years that make up Time.
R. Bradbury. And thunder struck

How organized is our life? Are certain events predetermined in it? What is predictable for many years to come, and what is not subject to any reliable forecasting even for short time intervals? nine0005

A person constantly has to deal with both ordered and disordered processes generated by various dynamic systems. We know that the Sun rises and sets every 24 hours and will continue to do so throughout our lives. After winter, spring always comes, and it is unlikely that it will ever be the other way around. Public services that supply us with light and heat, institutions and shops, as well as transport systems (buses, trolleybuses, metro, planes, trains) function more or less regularly. Violations of the rhythmic operation of these systems cause legitimate indignation and indignation of citizens. If failures occur repeatedly, they speak of chaos, expressing a negative attitude towards such phenomena. nine0005

But at the same time, there are processes that are well known for their unpredictability. For example, when tossing a coin, we never know for sure whether it will come up heads or tails. Such unpredictability is not alarming. It can lead to much more dramatic consequences when playing roulette, but those who like to tempt fate consciously take this risk.

Why are some processes predictable in their results, while others are not? Maybe we just do not have enough initial data for a good forecast? It is necessary to improve knowledge about the initial conditions - and everything will be in order, both with the coin and with the weather forecast. Laplace said: give me the initial conditions for the entire universe, and I will calculate its future. Laplace was wrong: he and his contemporaries did not know examples of deterministic dynamical systems whose behavior cannot be predicted for a long time. It was only at the end of the 19th century that the French mathematician Henri Poincaré first felt that this was possible. However, another three-quarters of a century passed before the era of rapid study of deterministic chaos began. nine0005

Dynamic systems can be conditionally divided into two types. For the former, the trajectories of motion are stable and cannot be significantly changed by small perturbations. Such systems are predictable - that is why we know that the Sun will rise tomorrow, in a year and in a hundred years. To determine the future in this case, it is sufficient to know the equations of motion and set the initial conditions. Small changes in the values ​​of the latter will only lead to an insignificant error in the forecast.

Another type includes dynamical systems whose behavior is unstable, so that any arbitrarily small perturbations quickly (on the time scale characteristic of this system) lead to a cardinal change in the trajectory. As Poincaré noted in his work "Science and Method" (1908), in unstable systems "an absolutely insignificant cause, eluding us due to its smallness, causes a significant effect that we cannot foresee. (...) Prediction becomes impossible, we have a random phenomenon in front of us." Thus forecasting for long periods loses all meaning.

The non-linear oscillatory circuit example discussed above shows that chaotic behavior with an unpredictable future can occur even in very simple systems. nine0005

Reconstruction of the past

So, predicting the future is not always possible. And what about the past? Is it always possible to reconstruct ("predict", unequivocally interpret) the past? It would seem that there should be no problems here. Since the trajectories move away from each other when moving forward, they must converge when moving backward. The way it is. However, the directions along which the convergence or divergence of trajectories in the phase space can occur are not one, but several. When moving both forward and backward, the trajectories can converge along one part of the directions, but diverge along the other. nine0005

The past is "not predictable"? Nonsense! After all, something has already happened. Everything is known... But let's think about it. If everything was so simple with the reconstruction of the past, how then could it happen that for some Nicholas II is still bloody, but for others a saint? And who is Stalin anyway: a genius or a villain? Let's digress for the time being from the problem of how free they were to make certain decisions, to what extent these decisions were predetermined by circumstances, and what could be the consequences of alternative decisions. Let us consider the historical process as the dynamics of some hypothetical chaotic system. Then, when trying to reconstruct the past, we will encounter a rapidly increasing number of options (trajectories) that correspond to the current state of the system. Only one of them corresponds to the real course of events. If you choose not him, but some other one, you will get an already distorted "version" of history. On the basis of what is the correct trajectory ("version") selected? The information we can rely on is the totality of available concrete facts. Trajectories that are incompatible with them are discarded. As a result, if there are enough reliable facts, there will be one trajectory that determines the only version of history. However, even for the recent past, there may be much more trajectories than reliable information - then an unambiguous interpretation of the historical process can no longer be made. And all this with a conscientious and respectful attitude to history and facts. Now add here the predilections of primary sources, the loss of some information over time, the manipulation of facts at the stage of interpretation (hushing up some, sticking out others, falsification, etc.) - and replacing black with white will not be such a difficult task. And what is most interesting is that, if necessary, the same interpreters after a while can easily assert the opposite. A familiar picture? nine0005

So, the dynamic nature of the "unpredictability" of the past is similar to the nature of the unpredictability of the future: the instability of the trajectories of a dynamic system and the rapid increase in the number of possible options as you move away from the starting point. In order to reconstruct the past, in addition to the dynamic system itself, information from this past is sufficient in quantity and reliable in quality. It should be noted that in different parts of the historical process, the degree of its chaos is different and can even drop to zero (a situation where everything essential is predetermined). Naturally, the less chaotic the system, the easier it is to reconstruct its past. nine0005

Is chaos manageable?

Chaos often gives birth to life.
G. Adams

At first glance, the nature of chaos makes it impossible to control it. In reality, the opposite is true: the instability of the trajectories of chaotic systems makes them extremely sensitive to control.

Let, for example, it is required to transfer the system from one state to another (to move the trajectory from one point of the phase space to another). The required result can be obtained within a given time by one or a series of subtle, insignificant perturbations of the system parameters. Each of them will only slightly change the trajectory, but after some time the accumulation and exponential amplification of small perturbations will lead to a significant correction of the motion. In this case, the trajectory will remain on the same chaotic attractor. Thus, systems with chaos demonstrate both good controllability and amazing plasticity: sensitively reacting to external influences, they retain the type of movement. nine0005

According to many researchers, it is the combination of these two properties that is the reason why chaotic dynamics is characteristic of the behavior of many systems of living organisms. For example, the chaotic nature of the heart rhythm allows it to respond flexibly to changes in physical and emotional stress, adjusting to them. It is known that the regularization of the heart rate leads after some time to death. One reason is that the heart may not have enough "mechanical strength" to compensate for external disturbances. In fact, the situation is more complicated. The ordering of the work of the heart serves as an indicator of a decrease in chaos in other related systems. Regularity indicates a decrease in the body's resistance to random environmental influences, when it is no longer able to adequately track changes and respond flexibly enough to them. nine0005

Obviously, any complex systems operating in a changing environment should have such plasticity and controllability. This is the guarantee of their safety and successful evolution.

From chaos to order

How is the integrity and stability of living organisms and other complex systems ensured if their individual parts behave chaotically?

It turns out that in addition to chaos in complex nonlinear systems, the opposite phenomenon is also possible, which could be called antichaos . In the event that chaotic subsystems are connected with each other, their spontaneous ordering ("crystallization") can occur, as a result of which they will acquire the features of a single whole. The simplest variant of such ordering is chaotic synchronization , when all subsystems connected with each other move albeit chaotically, but equally, synchronously. Chaotic synchronization processes can occur not only in animals and humans, but also in larger structures - biocenoses, public organizations, states, transport systems, etc.

What determines the possibility of synchronization? First, the behavior of each individual subsystem: the more chaotic, "independent" it is, the more difficult it is to make it "reckon" with other elements of the ensemble. Secondly, by the total strength of the connection between subsystems: its increase suppresses the tendency to "independence" and can, in principle, lead to ordering. At the same time, it is important that the links are global , that is, they exist not only between neighboring, but also between elements that are far from each other. nine0005

In real systems, which include a large number of subsystems, communication is carried out at the expense of material or information flows. The more intense they are, the greater the chance that the elements will behave in a coordinated manner, and vice versa. For example, in the state, the role of connecting flows is played by transport, post, telephone, etc. Therefore, an increase in tariffs for these services, in the case when it leads to a decrease in the corresponding flows, weakens the integrity of the state and contributes to its destruction. nine0005

It follows from the theory of chaotic synchronization that the coordinated operation of individual parts of a complex system can be ensured by one of its elements, called a pacemaker or "pacemaker". Being connected in a unilateral way with all the components of the system, it "manages" their movement, imposing its own rhythm. If, at the same time, we make it so that the individual subsystems are not connected to each other, but only to the pacemaker, we will get the case of an extremely centralized system. In a state, for example, the role of "rhythm leader" is performed by the central government and ... the mass media, operating throughout or a significant part of the country's territory. Today, this is especially true of electronic media, since they are far superior to others in terms of mobility and general information flow. Understanding this intuitively, the central government tries to keep the media under control, and also limits the influence of each of them individually. Otherwise, she will no longer govern the state. nine0005

Here we touched on a very important issue. Since the average strength of connections is a total parameter, which includes both material and informational connections, this means that the weakening of some of them can be compensated by the strengthening of others. The simplest example is the replacement of real goods with paper or even electronic money. In this case, the supplier, in fact, instead of a material product, receives information about a change in his account - and such an exchange suits him perfectly. In the same way, huge sums of money are gained or lost daily through stock exchanges, which, in the end, someone must make up for in real products or services. nine0005

How can the destruction of the synchronized state occur?

We have already mentioned one possibility. It's weakening ties. Another reason is the inadequate influence of the "rhythm leader" on the ensemble. Indeed, if the "rhythm" dictated by the pacemaker is too contrary to the natural behavior of the system's components, then even with a sufficient strength of connection, he will not be able to impose his line of behavior on the ensemble. However, the previous behavior will also not be preserved. As a result, synchronization will be destroyed. nine0005

Fractality and stability

We have already seen that the theory of dynamic chaos can be applied to many systems, including the state and society as a whole. And what role does the fractal structure of chaos play in this? After all, the image of chaos in the phase space - a strange attractor - geometrically represents a fractal. Despite the fact that each individual chaotic trajectory is extremely sensitive to the slightest perturbations, the strange attractor (the totality of all possible trajectories) is a very stable structure. Thus, dynamic chaos is like a two-faced Janus: on the one hand, it manifests itself as a model of disorder, and on the other, as stability and order on different scales. nine0005

If you think about it, it is easy to see that in society, as in nature, many systems are built according to the principle of fractals: some complexes are formed from small elements, they, in turn, serve as elements for larger complexes, etc. How, for example, are organized viable economic and production structures? Two extreme positions: large transnational companies and "small business". Each of them individually is not viable. Large companies, possessing enormous economic power, are inactive and cannot quickly respond to changes in the surrounding economic environment. "Small business" is not able to solve major problems, to ensure the development of infrastructure. Where is the golden mean? In medium-sized enterprises? Not at all. A stable economic infrastructure is provided (with the necessary pumping of the necessary resources) by a set of different-scale (here it is a fractal!) Economic objects that form a pyramid. At its base there are many small companies and firms, above the pyramid the size of enterprises gradually increases, and their number, respectively, decreases, and, finally, at the top are the largest companies. Such a structure is typical, for example, for the US economy. At the same time, small enterprises are the most mobile: they are often born and die, being the main suppliers of new ideas and technologies. Innovations that have received sufficient development allow a number of enterprises to grow to the next level or transfer (sell) the accumulated innovations to larger companies. With sufficient susceptibility of the environment, such a mechanism is able to create new industries and economies in a few years. Not without reason in the so-called "new economy" the bulk of even large enterprises are companies that 15-20 years ago either did not exist at all or were in the category of small ones. nine0005

Another example. During perestroika, a lot was written and said about the "wrong" structure of the USSR, in which the state had a complex hierarchical structure, organized according to the principle of nesting dolls. What was offered instead? Each nation has its own native army, its own language, its own "elite", its tribal leaders. That sounds good. And now look at how this idea turned out for many peoples of the former USSR and Yugoslavia... From the point of view of the theory of stability, the idea of ​​a homogeneous structure of the Russian state is the idea of ​​a loser. Why? The nesting doll principle is, in fact, a fractal principle, thanks to which a chaotic system acquires structure and stability. The USSR and the Russian Empire were built on the principle of fractal systems, and this ensured their stability as states. At different levels, natural state, ethnic, territorial and other formations with well-established mechanisms of internal functioning, with their own rights and obligations, were interspersed in the overall system. nine0005

Chaos generates information

We have already established that the behavior of chaotic systems cannot be predicted over long time intervals. As you move away from the initial conditions, the position of the trajectory becomes more and more uncertain. From the point of view of information theory, this means that the system itself generates information, and the rate of this process is the higher, the greater the degree of chaos. From here, according to the theory of chaotic synchronization considered earlier, an interesting conclusion follows: the more intensively the system generates information, the more difficult it is to synchronize it, to make it behave in some other way. nine0005

This rule seems to be true for any systems that produce information. For example, if a certain creative team generates a sufficient number of ideas and and is actively working on ways to implement them, it is more difficult for him to impose from outside some line of behavior that is inadequate to his own views. And vice versa, if, in the presence of the same material flows and resources, the team behaves passively in the informational sense, does not create ideas or does not put them into practice - in other words, follows the principle "... warm and damp" - then it is very easy to subordinate it . nine0005

Chaotic computers

What do we lack in modern computers? If a living organism must have elements of chaotic behavior in order to exist in a changing environment, then it can be assumed that artificial systems capable of adequately interacting with a changing environment must be chaotic to some extent. Modern computers are not. They are closed systems with a very large but finite number of states. Perhaps in the future, on the basis of dynamic chaos, computers of a new type will be created - systems that are open from a thermodynamic point of view, capable of adapting to environmental conditions. nine0005

However, even today chaotic algorithms can be successfully used in computer technologies for storing, searching, and protecting information. When solving some problems, they turn out to be more effective than traditional methods. This applies in particular to working with multimedia data. Unlike texts and programs, multimedia information requires a different way of organizing memory. The blue dream of users is the ability to search for a melody, video or necessary photos not by their attributes (directory and file name, creation date, etc.), but by content or association, so that, for example, a fragment of a melody can be used to find and play a musical work. It turns out that such an associative search can be carried out using technologies based on deterministic chaos. How? nine0005

We have already discussed the generation of information by chaotic systems. Now let's ask ourselves a question: is it possible to match the trajectory with specific data written in the form of a certain sequence of characters? Then part of the trajectories of the system would be in one-to-one correspondence with our information sequences. And since each trajectory is a solution to the equations of motion of the system under certain initial conditions, then any sequence of symbols could be restored by solving these equations, setting a small fragment of it as initial conditions. Thus, the possibility of an associative search for information, that is, a search by content, would appear. nine0005

A team of employees of our institute created mathematical models for recording, storing and retrieving information using the trajectories of dynamic systems with chaos. Although the algorithms seemed very simple, their potential information capacity greatly exceeded the amount of information available on the Internet. The development of the idea led to the creation of a technology that allows processing any type of data: images, text, digital music, speech, signals, etc. (RF Patent 2050072, US Patent 5774587, Canada Patent 2164417). nine0005

An example of using the technology is the Forget-Me-Not software package designed to work with archives of unstructured information both on personal computers and on information servers. "Forget-Me-Not" is implemented as a search engine running under standard Internet browsers such as Netscape and Explorer. All information in the archive is recorded and stored as trajectories of a chaotic system. To search for the necessary documents, the user composes a query by typing in an arbitrary form several lines of text related to the content of the required document. In response, the system will issue the desired document if the input information is sufficient for its unambiguous search, or it will offer a set of options. If necessary, you can get a facsimile copy of the found document. The presence of errors in the query does not significantly affect the quality of the search. nine0005

Additional information on the Forget-Me-Not complex, as well as a demo version of the program, can be obtained at http://www.cplire.ru.

Communication through chaos

Most modern communication systems use harmonic oscillations as the information carrier. The information signal in the transmitter modulates these oscillations in amplitude, frequency or phase, and in the receiver the information is extracted using the inverse operation - demodulation. The imposition of information on the carrier is carried out either by modulating the already formed harmonic oscillations, or by controlling the parameters of the generator during its operation. nine0005

Similarly, it is possible to modulate a chaotic signal. However, the possibilities here are much broader. Harmonic signals have only three controllable characteristics (amplitude, phase and frequency). In the case of chaotic oscillations, even small variations in the value of the parameter of one of the elements of the source of chaos lead to changes in the nature of the oscillations, which can be reliably recorded by instruments. This means that sources of chaos with variable element parameters potentially have a large set of schemes for inputting an information signal into a chaotic carrier (modulation schemes). In addition, chaos fundamentally has a wide frequency spectrum, that is, it refers to broadband signals, the interest in which in radio engineering is traditionally associated with their greater information capacity compared to narrowband oscillations. A wide carrier bandwidth allows you to increase the speed of information transfer, as well as increase the stability of the system to disturbing factors. Chaos-based broadband and ultra-wideband communication systems have potential advantages over traditional wide spectrum systems in such defining parameters as ease of hardware implementation, energy efficiency and information transfer rate. Chaotic signals can also serve to mask information transmitted over a communication system without using spectrum spreading, that is, when the frequency bands of the information and transmitted signals coincide. nine0005

The combination of these factors stimulated active research into chaotic communication systems. At present, several approaches have already been proposed to expand the spectrum of information signals, to build transmitters and receivers that are simple in architecture.

One of the latest ideas in this direction is the so-called direct chaotic communication schemes. In a direct chaotic communication scheme, information is introduced into a chaotic signal generated directly in the radio or microwave wavelength range. Information is introduced either by modulating the parameters of the transmitter, or by imposing it on a chaotic carrier after it has been generated. Accordingly, the extraction of an information signal from a chaotic one is also carried out in the region of high or ultrahigh frequencies. Estimates show that broadband and ultra-wideband direct chaotic communication systems are capable of providing information transfer rates from tens of megabits per second to several gigabits per second. At the Institute of Radio Engineering and Electronics of the Russian Academy of Sciences, experiments have already been carried out on direct chaotic transmission of information at a speed of up to 70 Mbps. nine0005

Chaos and computer networks

In communication schemes, chaos can be used as a carrier of information, as a dynamic process that ensures the transformation of information to a new form, and, finally, as a combination of both. A device that converts a signal in a transmitter from one type to another using chaos is called a chaotic encoder . With its help, you can change information in such a way that it will be inaccessible to an outside observer, but at the same time it will be easily returned to its original form by a special dynamic system - by a chaotic decoder located on the receiving side of the communication system.

In what processes can chaotic coding be used?

Firstly, it can be used to organize a common information space in a fundamentally new way, creating large open user groups in it - subspaces. Within each group, its own "language" of communication is introduced - rules, protocols and other signs of this "information subculture" that are common for all participants. For those wishing to learn this "language" and become a member of the community, there are relatively easy means of access. At the same time, it will be difficult for outside observers to participate in such an exchange. Thus, chaotic coding can serve as a means of structuring the "population" of a common information space. nine0005

Secondly, in a similar way, you can organize multi-user access to information. The presence of the global Internet and the main information flows (Highways) implies the existence of common protocols that ensure the passage of information through single channels. However, within certain groups of participants (for example, within corporate networks), there is an urgent need to deliver information to specific consumers, without allowing access to "foreign" participants. Chaotic coding methods are a convenient means of organizing such virtual corporate networks. In addition, they can be used directly to ensure a certain level of confidentiality of information, moving into the area of ​​traditional cryptography. nine0005

Finally, another function of chaotic coding is very relevant in connection with the development of e-commerce and the aggravation of the copyright problem on the Internet. In particular, this applies to the sale of multimedia goods (music, video, digital photography, etc. ) through the network. On the basis of deterministic chaos, it is possible to provide such a way to protect copyrights and intellectual property rights as a decrease in the quality of an information product with general access. For example, music tracks encoded with chaos will be distributed on the network without any restrictions, so that every user can use them. However, when listening without a special decoder, the sound quality will be poor. What is the point of such an approach? The disseminated information remains open and is not subject to restrictions imposed by the use of cryptographic protection methods. In addition, a potential buyer has the opportunity to get acquainted with the product, and only then decide whether to purchase its high-quality version. nine0005

It should be noted that the above functions of chaotic coding far from exhaust the potential possibilities of its application in modern information technologies. In the course of further study and development of this problem, apparently, new facets and promising areas of use may open up.

Thus, the use of dynamic chaos and fractals in information technology is not exotic, as it might have seemed a few years ago, but a natural way to develop new approaches to creating systems that work effectively in a changing environment. nine0005

EXISTENTIALISM – Department of Philosophy

EXISTENTIALISM - philosophy, the course of the 20th century .. bringing to the fore the absolute uniqueness of human existence, which does not allow expression in the language concepts. The origins of existentialism as a special direction of thought are contained in Kierkegaard's teachings. It was he who first formulated the antithesis of "existence" and "systems", meaning by the latter Hegel's system. Contrary to panlogism, dissolving being in thinking, i.e., confident that being to the smallest details are permeable to thought, without a trace fit into the concept, Kierkegaard asserts that existence (is that which always eludes understanding through abstractions. From this follows the thesis of the inapplicability scientific method in self-knowledge of man. Existence is "internal", which constantly passes into external, objective being. Since the subject being expresses the “inauthentic existence” of a person, the acquisition '"existence presupposes a decisive choice, through which a person passes from the contemplative-sensory way of being, determined external environmental factors, to "himself", the one and only. This path of Kierkegaard, in contrast to Hegel's speculative dialectic, called "existential dialectics" He singled out three fundamentals. ascending stage movement towards “true existence”, i.e., towards existence: aesthetic, ethical and religious. The principle of the aesthetic stage is the determination by external, t, i.e. orientation towards “enjoyment”. Here, the choice is made only in the primitive form, because only the object is selected, and the attraction itself is predetermined by the directly sensual element human life. The principle of the ethical stage is duty. It's already self-determination of the subject, but still in a purely rational way, according to the precepts of the moral law. Abstraction ^{the moral law is completely overcome only on religious stage of existence, when a person, by an incredible effort of will, refuses former habits of existence, accepts with his whole being Suffering as a principle of existence and thereby joins the share of the crucified Christ. Kierkegaard's views have long existed as an isolated phenomenon. spiritual life of the Scandinavian countries, Philos, became a current of E. only after the 1st world war, which shook the entire socio-economic European style. about-va, and above all its official liberal Christian ideology. An essential ingredient of this ideology constituted an enlightening conviction in the invincibility of the progressive movement of mankind with the progress of science and civilization. 1st and especially 2nd World War with the genocide organized by the Nazis, they found a clear lack of humanity at the very foundation scientific and technological civilization - in relations between people. Then it's time for E. to-ry becomes the most popular current of thought in the West. Europe in the 40s-60s of our century Manifesto of this direction, became books and articles Jaspers, Marcel, Heidegger. written back in the 1920s and 1930s, but made public, phenomenon in the first decades after the victory over fascism. New push development gave activity Sartre and Camus, who comprehended the experience of the fight against fascism and politicized E., linking it with burning social and political problems of the postwar period. To analyze E. it is necessary to single out the invariant content of the constructions of representatives of this currents. First of all, E. is ontology, doctrine of being, not about what a person “should” or “should” do. Genetic character E. is emphasized by all its adherents without exception. it means that existential thinking unfolds exclusively in the sphere of being, and all other traditional philosophies. problems become secondary value, as particular consequences from the decision of the main. ontological problem. This main the problem is the definition of existence in the general structure of being, i.e. concretization of the ontological nature of human reality in relation to the rest of the principles of the universe. Main ontological definition existence - "being-between" - belongs to Kierkegaard and is shared by all representatives of E. This from the very beginning emphasizes the intermediate the nature of human reality, its fundamental lack of independence, dependence from something else that is no longer human. (That's why erroneous unconditional attribution of E. to “subjective idealism”) The nature of this Existentialists understand the “other” in different ways. Religious existentialists (K A. Berdyaev, Jaspers. Marseille, Tillich) define this otherness as “transcendence”, revealed in an act of faith. The divine is interpreted in the spirit of “ and pophatic theology”, which does not recognize any positive definitions of a deity and delimiting it from the world by a whole system of denials. Definition t ranscence through negation is especially characteristic of Heidegger, to-rogo transcendence acts as "nothing" - an abyss opened in a dense an array of realities. Christian thinkers (Berdyaev, Marcel) characteristics of transcendence bears the imprint of the values ​​of faith, hope, love; so, for example, according to Marcel, Bos is the “absolute You” - - the most intimate and reliable friend. L. Shestov, who is close to Judaism, has echoes Old Testament sentiments. Jaspers, generalizing the achievements of the “axial time”, and to-rum arose osn. world religions, seeks to highlight a certain core of philosophy. nine0043 Faith". non-binding k.-l. certain sgeyo. For all differences among themselves, religious existentialists do not think the existence of the divine outside an act of faith, i.e. they reject the dogmatic postulation of existence God as a precondition for faith. The Divine really exists only in an act of faith, and simultaneously with his appearance in the horizon of human existence is possible achieve "true existence". On the contrary, outside the aspiration to transcendence, degradation of human reality takes place, its depersonalization and dissolving in the routine of everyday life. But existence is existential characteristic of human reality, therefore, even at the bottom of the fall, a person vaguely feels his participation in the higher, no matter how humbled he may be in social life. Hence the phenomenological description characteristic of E. situations of spiritual crisis, in which an impersonal being manifests acute sense of wrongness, senselessness, unworthiness of your being. It is not at all accidental that there are many representatives of E., starting from Kierkegaard, with equal ease used the philosopher's pen, analyzing the "existentials" of human reality, and with the pen of an artist, depicting real life situations in which these abstract existentials” appear in the flesh. Rapprochement Lit. and philosophy in the context of E. facilitated by the existentialists' assimilation of the phenomenological method nine0043 Husserl, '' whose favorite student for some time was Heidegger. Heidegger rethought the phenomenological method and applied it to the study of existence, which he interpreted as “intentional being”, “being-in-the-world”. Following him, a similar operation was performed by Sartre and before some degree of Merleau-Ponty. The phenomenological method allowed turn E. into a systematic ontology that describes reality in kind of categorical order. Disregarding the individual originality of thinkers, the categorical the structure of late E. can be presented in form of the following ontological triads: “world-being-in-world-being”. Existence is the middle term of the triad, the intermediate a link that connects the otherworldly being with the “world” as the arena of everyday impersonal existence. Orientation of human reality ' on the world means inauthentic existence, “abandonment”, and striving for the otherworldly, “calling to being”—true existence. The urge for true existence is contained in such phenomena like “fear” (Jaspers, Heidegger), “existential anxiety”, “nausea” (Sartre), "boredom" (Camus). "Fear" in an existential sense is by no means cowardice, not physical fear, but metaphysical horror - amazing human insight. What is important here is not the psychological content of the phenomenon (fear, but its ontological meaning, which lies in the fact that a gaping the abyss of being, which he did not know before, calmly vegetating in the hustle and bustle of everyday affairs. Now there is no rest, only the risk of a decision remains, which does not guarantee success. it and there is a “genuine existence”, which is much more difficult to endure than a thoughtless existence within the established order of things. T. arr., religious E. calls a person from the world to God, to self-deepening, allowing you to find a new, “transcendental” dimension of being. nine0005}

Self-deepening eat together with that, and the expansion of the boundaries of the individual I, as it explodes selfish isolation and vast horizons of communication with their era and eternity. A completely different attitude in the atheistic E. Sartre and Camus. Here the main ontological scheme acquires a different content. God is a “contradiction in definition”, i.e., a contradictory a combination of incompatible characteristics: consciousness, which is always repelled from being, and autonomous, self-sufficient, self-equal being. The latter cannot possibly have consciousness, because then it would inevitably lose its identity with itself. If it is true, then absolute being can in no way be a person, i.e. God cannot be exist. For Sartre, absolute being is interpreted in a completely materialistic way, although materiality looks extremely unattractive to him - in the form of a giant, all-filling dump of gelatinous mucus. With such a characterization of absolute being, “true existence” Sartre could no longer interpret as striving towards being. It comes from the opposition of consciousness and being, which is very reminiscent of Cartesian dualism of spirit and matter, with the only difference being that consciousness is identified by him with negation, repulsion from being, “drilling” into him "holes". Inauthentic existence strives for “positivity”, for boundless self-affirmation at the expense of others, which, according to Sartre, yavl. "wanting to be God" e. Nietzsche's project of the superman. Genuine same ^{existence, as opposed to the insane lust for power, is the recognition inalienable freedom of another} along with my own freedom - so that every act my choice has become a choice for all and in the name of all. Highlighting the meaning choice and the role of the subject's initiative, Sartre follows, Fichte, and demanding that the individual act have a universal human content—Kant. Somewhat differently defines the true existence of Camus in The Rebellious Man. From his point of view, it is continuous ascesis of negation, absolute non-conformism, disagreement with everything positive, rejection everything that exists, both individually and as a whole. logical conclusion this idea became the concept of the “Great Refusal” Marcuse. So atheistic E. became a philosopher.}

• 
  Yoga for ptsd
• 
  Common questions about dreams
• 
  Young girls attracted to older men
• 
  Spring break hard
• 
  Highest dosage of ritalin
• 
  Ocd confessing past mistakes
• 
  Difference between adhd and dyslexia
• 
  Do negative thoughts come true
• 
  How do i stop eating
• 
  What does it mean when you feel empty inside
• 
  Listen yourself quotes