What is the purpose of correlational research
Correlational Research | When & How to Use
Published on July 7, 2021 by Pritha Bhandari. Revised on December 5, 2022.
A correlational research design investigates relationships between variables without the researcher controlling or manipulating any of them.
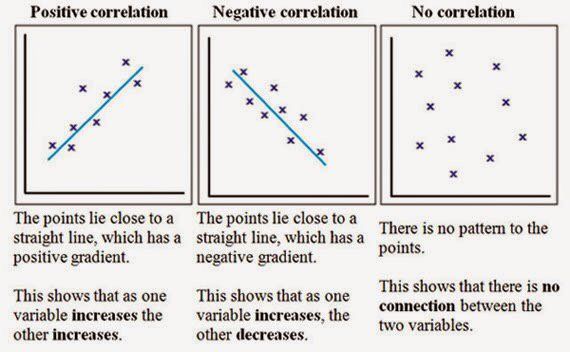
A correlation reflects the strength and/or direction of the relationship between two (or more) variables. The direction of a correlation can be either positive or negative.
| Positive correlation | Both variables change in the same direction | As height increases, weight also increases |
|---|---|---|
| Negative correlation | The variables change in opposite directions | As coffee consumption increases, tiredness decreases |
| Zero correlation | There is no relationship between the variables | Coffee consumption is not correlated with height |
Table of contents
- Correlational vs.
experimental research
- When to use correlational research
- How to collect correlational data
- How to analyze correlational data
- Correlation and causation
- Frequently asked questions about correlational research
Correlational vs. experimental research
Correlational and experimental research both use quantitative methods to investigate relationships between variables. But there are important differences in data collection methods and the types of conclusions you can draw.
| Correlational research | Experimental research | |
|---|---|---|
| Purpose | Used to test strength of association between variables | Used to test cause-and-effect relationships between variables |
| Variables | Variables are only observed with no manipulation or intervention by researchers | An independent variable is manipulated and a dependent variable is observed |
| Control | Limited control is used, so other variables may play a role in the relationship | Extraneous variables are controlled so that they can’t impact your variables of interest |
| Validity | High external validity: you can confidently generalize your conclusions to other populations or settings | High internal validity: you can confidently draw conclusions about causation |
When to use correlational research
Correlational research is ideal for gathering data quickly from natural settings. That helps you generalize your findings to real-life situations in an externally valid way.
That helps you generalize your findings to real-life situations in an externally valid way.
There are a few situations where correlational research is an appropriate choice.
To investigate non-causal relationships
You want to find out if there is an association between two variables, but you don’t expect to find a causal relationship between them.
Correlational research can provide insights into complex real-world relationships, helping researchers develop theories and make predictions.
ExampleYou want to know if there is any correlation between the number of children people have and which political party they vote for. You don’t think having more children causes people to vote differently—it’s more likely that both are influenced by other variables such as age, religion, ideology and socioeconomic status. But a strong correlation could be useful for making predictions about voting patterns.To explore causal relationships between variables
You think there is a causal relationship between two variables, but it is impractical, unethical, or too costly to conduct experimental research that manipulates one of the variables.
Correlational research can provide initial indications or additional support for theories about causal relationships.
ExampleYou want to investigate whether greenhouse gas emissions cause global warming. It is not practically possible to do an experiment that controls global emissions over time, but through observation and analysis you can show a strong correlation that supports the theory.To test new measurement tools
You have developed a new instrument for measuring your variable, and you need to test its reliability or validity.
Correlational research can be used to assess whether a tool consistently or accurately captures the concept it aims to measure.
ExampleYou develop a new scale to measure loneliness in young children based on anecdotal evidence during lockdowns. To validate this scale, you need to test whether it’s actually measuring loneliness. You collect data on loneliness using three different measures, including the new scale, and test the degrees of correlations between the different measurements. Finding high correlations means that your scale is valid.
Finding high correlations means that your scale is valid.
Prevent plagiarism. Run a free check.
Try for freeHow to collect correlational data
There are many different methods you can use in correlational research. In the social and behavioral sciences, the most common data collection methods for this type of research include surveys, observations, and secondary data.
It’s important to carefully choose and plan your methods to ensure the reliability and validity of your results. You should carefully select a representative sample so that your data reflects the population you’re interested in without research bias.
Surveys
In survey research, you can use questionnaires to measure your variables of interest. You can conduct surveys online, by mail, by phone, or in person.
Surveys are a quick, flexible way to collect standardized data from many participants, but it’s important to ensure that your questions are worded in an unbiased way and capture relevant insights.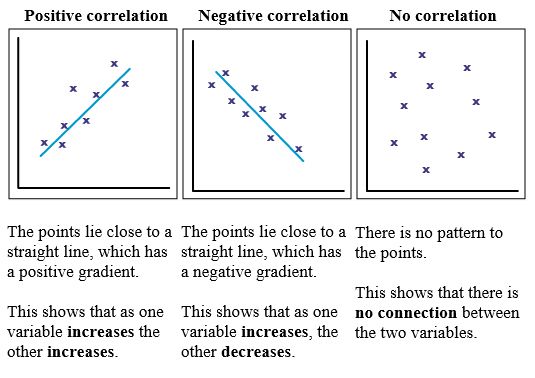
Naturalistic observation
Naturalistic observation is a type of field research where you gather data about a behavior or phenomenon in its natural environment.
This method often involves recording, counting, describing, and categorizing actions and events. Naturalistic observation can include both qualitative and quantitative elements, but to assess correlation, you collect data that can be analyzed quantitatively (e.g., frequencies, durations, scales, and amounts).
Naturalistic observation lets you easily generalize your results to real world contexts, and you can study experiences that aren’t replicable in lab settings. But data analysis can be time-consuming and unpredictable, and researcher bias may skew the interpretations.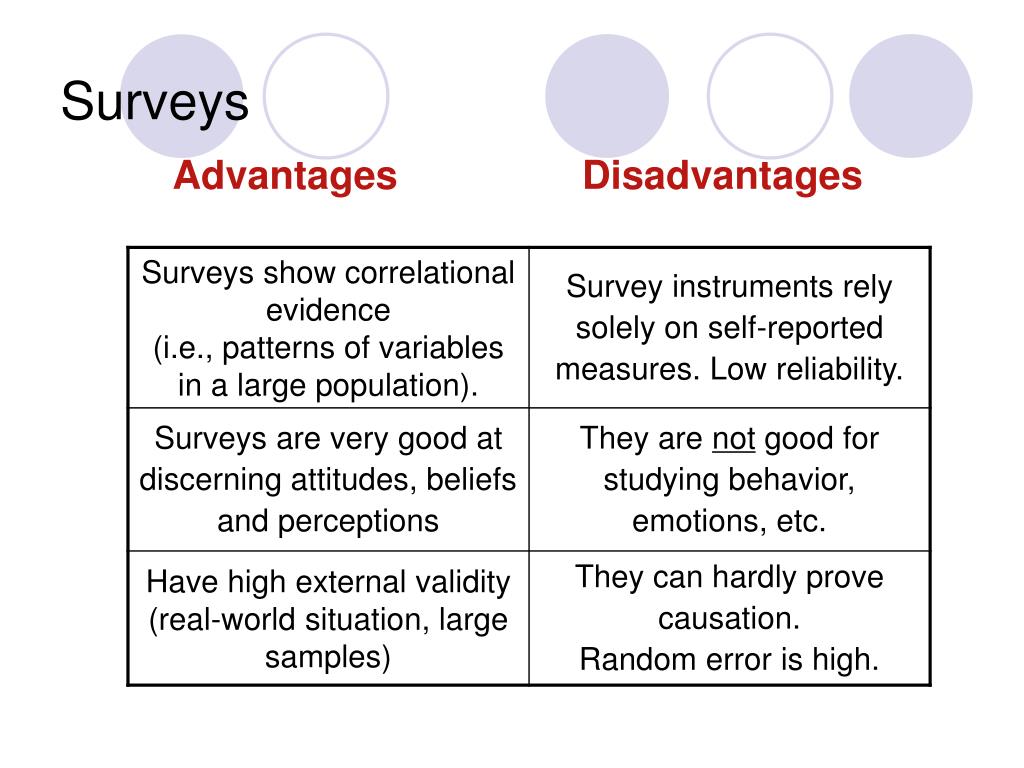
Secondary data
Instead of collecting original data, you can also use data that has already been collected for a different purpose, such as official records, polls, or previous studies.
Using secondary data is inexpensive and fast, because data collection is complete. However, the data may be unreliable, incomplete or not entirely relevant, and you have no control over the reliability or validity of the data collection procedures.
ExampleTo find out if working hours are related to mental health, you use official national statistics and scientific studies from several different countries to combine data on average working hours and rates of mental illness. You statistically analyze the data to see if countries that work fewer hours have better mental health outcomes.
You statistically analyze the data to see if countries that work fewer hours have better mental health outcomes.How to analyze correlational data
After collecting data, you can statistically analyze the relationship between variables using correlation or regression analyses, or both. You can also visualize the relationships between variables with a scatterplot.
Different types of correlation coefficients and regression analyses are appropriate for your data based on their levels of measurement and distributions.
Correlation analysis
Using a correlation analysis, you can summarize the relationship between variables into a correlation coefficient: a single number that describes the strength and direction of the relationship between variables. With this number, you’ll quantify the degree of the relationship between variables.
The Pearson product-moment correlation coefficient, also known as Pearson’s r, is commonly used for assessing a linear relationship between two quantitative variables.
Correlation coefficients are usually found for two variables at a time, but you can use a multiple correlation coefficient for three or more variables.
Regression analysis
With a regression analysis, you can predict how much a change in one variable will be associated with a change in the other variable. The result is a regression equation that describes the line on a graph of your variables.
You can use this equation to predict the value of one variable based on the given value(s) of the other variable(s). It’s best to perform a regression analysis after testing for a correlation between your variables.
Correlation and causation
It’s important to remember that correlation does not imply causation. Just because you find a correlation between two things doesn’t mean you can conclude one of them causes the other for a few reasons.
Directionality problem
If two variables are correlated, it could be because one of them is a cause and the other is an effect. But the correlational research design doesn’t allow you to infer which is which. To err on the side of caution, researchers don’t conclude causality from correlational studies.
But the correlational research design doesn’t allow you to infer which is which. To err on the side of caution, researchers don’t conclude causality from correlational studies.
Third variable problem
A confounding variable is a third variable that influences other variables to make them seem causally related even though they are not. Instead, there are separate causal links between the confounder and each variable.
In correlational research, there’s limited or no researcher control over extraneous variables. Even if you statistically control for some potential confounders, there may still be other hidden variables that disguise the relationship between your study variables.
There are many other variables that may influence both variables, such as average income, working conditions, and job insecurity. You might statistically control for these variables, but you can’t say for certain that lower working hours reduce stress because other variables may complicate the relationship.
Although a correlational study can’t demonstrate causation on its own, it can help you develop a causal hypothesis that’s tested in controlled experiments.
Frequently asked questions about correlational research
- What is a correlation?
-
A correlation reflects the strength and/or direction of the association between two or more variables.
- A positive correlation means that both variables change in the same direction.
- A negative correlation means that the variables change in opposite directions.
- A zero correlation means there’s no relationship between the variables.
- What’s the difference between correlational and experimental research?
-
Controlled experiments establish causality, whereas correlational studies only show associations between variables.
- In an experimental design, you manipulate an independent variable and measure its effect on a dependent variable.
 Other variables are controlled so they can’t impact the results.
Other variables are controlled so they can’t impact the results. - In a correlational design, you measure variables without manipulating any of them. You can test whether your variables change together, but you can’t be sure that one variable caused a change in another.
In general, correlational research is high in external validity while experimental research is high in internal validity.
- In an experimental design, you manipulate an independent variable and measure its effect on a dependent variable.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bhandari, P. (2022, December 05). Correlational Research | When & How to Use. Scribbr. Retrieved March 29, 2023, from https://www.scribbr.com/methodology/correlational-research/
Cite this article
Is this article helpful?
You have already voted. Thanks :-) Your vote is saved :-) Processing your vote...
Thanks :-) Your vote is saved :-) Processing your vote...
Pritha has an academic background in English, psychology and cognitive neuroscience. As an interdisciplinary researcher, she enjoys writing articles explaining tricky research concepts for students and academics.
Correlational Research Designs
Purpose of Correlational ResearchUnlike the other research designs we will study in this course, correlational research can have either of two purposes. One purpose for doing correlational research is to determine the degree to which a relationship exists between two or more variables. Notice that I did NOT say cause-and-effect relationship. Correlational research designs are incapable of establishing cause-and-effect. What's the difference? Well, it's really quite simple. Variables can relate to one another without one causing the other to occur. Here's a simple example: When you move a light switch to a certain position, the lights in the room come on; when you move the light switch to the opposite position, the lights go off. There is a relationship between moving the light switch and the lights going on and off. However, the light switch doesn't cause the lights to go on and off. The second purpose for correlational research is to develop prediction models to be able to predict the future value of a variable from the current value of one or more other variables. A common prediction model used in education is the use of college entrance exam scores to help predict a prospective student's success in college. Colleges and universities work hard to develop the best prediction models they can to ensure that the most potentially successful students are admitted. To increase the predictive power of their models, they use correlational research methods, some of which we'll discuss a little later in this lesson. How to Identify This Type of DesignCorrelational research studies are almost always given away by the purpose statement (or hypothesis or objective). Usually somewhere in these statements will appear the phrase "determine the relationship between ... ." That's the clue that this is a correlational design. Description of a Correlation CoefficientBefore getting into the different statistics, let's make sure you understand what a correlation coefficient is. A correlation coefficient can take on a value anywhere between -1 and +1 (including zero). The sign of the coefficient simply means whether the correlation is direct (positive) or inverse (negative). The strength of the coefficient is determined by its numerical value. That is, a correlation coefficient of -.75 and one of . A direct (positive) correlation occurs when variable B increases as variable A increases, and variable B decreases as variable A decreases. An example of a direct correlation is the relationship between the height of a column of mercury in a glass tube (a thermometer) and the ambient air temperature. An inverse (negative) correlation occurs when variables A and B act opposite to each other (when A increases, B decreases and vice versa). For example, consider the relationship between fatigue and rest. The more rest one gets, the less fatigued he/she is, and vice versa (usually). "Usually" is an important word when we speak of correlations, because there are very, very few variables (if any) that correlate perfectly with each other. Consequently, the vast majority of correlations are less than 1 (or greater than -1), and are typically reported in decimal form. 0.7 to 1.0 -- strong correlation Statistical Significance of Correlation CoefficientsWe discussed the concept of statistical significance in
Week 3. We learned that when the result of a statistical test is significant, it means that it would not occur by chance more often than a certain percentage of time (5 times, or 1 time, out of 100). We can apply this concept to correlation coefficients too. But, it sometimes confuses students. So, let't take a moment to clarify it. The value of a correlation coefficient (from the previous paragraph) has no bearing on whether or not it is statistically significant. A Quick Look at Bivariate Correlational StatisticsThere are two categories of correlational statiistics: bivariate (two-variables) and multi-variate (many variables). Correlation coefficients used to satisfy the first of the purposes mentioned above (to identify the strength and direction of a relationship between variables) are bivariate in nature. That means that we can use these statistics to correlate only two variables at a time. The multi-variate correlational statistics are used to support the second purpose (to develop prediction models). They're a lot more complicated, so we won't go into much detail about them. We'll deal with them in the next section. For now, let's look at bivariate correlational statistics. In your text, Table
12.3 on page 273 displays ten different bivariate statistics. Can you tell which one(s) is(are) parametric? Check your answer if you're not sure. From our discussion of statistical tools in Week 3, recall that we discussed 4 primary data types: ratio and interval (collectively referred to as continuous), ranks, and nominal (or categorical). There appears to be two new types in this table: artificial and true dichotomies. Why are there so many different coefficients? To fit nearly every data combination. Let's say, for instance, you wanted to measure the degree of correlation (or relationship) between students' academic achievement on a standardized 12th grade math test and their IQ scores as measured by the Stanford Binet (testing the hypothesis that higher IQs are positively related to achievement test scores). What would be the most appropriate correlation coefficient to use? Your answer should go something like this: "Since academic achievement test scores and IQ test scores are both continuous, I would use either a Pearson r (product moment correlation) or an eta coefficient. Let's try another example. Say you wanted to determine the relationship between hair color (say blonde, brunette, and redhead) and academic achievement in math (to test the hypothesis that blondes are better at math than brunettes or redheads). What statistic would be most appropriate? Well, we know that academic achievement is a continuous variable. We should relaize that hair color is a categorical variable (with only three categories in this example). Looking through the table, however, we can't find a correlation coefficient that works with this combination of data types. Now we take advantage of a technique known as data reduction. Recall back to Week 3 when I listed the four data types in the following order:
 So, we should reduce our continuous (achievement) data to categorical data. That's actually pretty easy. We can change the achievement (typically percentage or raw) scores to letter grades (A, B, C, D, F), which are categorical. So, we should reduce our continuous (achievement) data to categorical data. That's actually pretty easy. We can change the achievement (typically percentage or raw) scores to letter grades (A, B, C, D, F), which are categorical.
So, what we've seen so far is that even though there isn't a correlation coefficient for every possible data pair. It is possible, through data reduction, to create a data set for which there is an appropriate correlational statistic. In the next section we'll talk just a little about the multivariate correlational statistics used in prediction studies. A Closer Look at Prediction StudiesThe premise behind prediction studies in social science research is that the degree to which variable A correlates with variable B allows us to make a prediction, at some level of confidence, about the value of variable B based on the value of variable A. Notice that prediction is not the same as cause-and-effect. What determines how well one variable can predict another is something called common (or explained or shared) variance. The way to determine the amount of common variance existing between two variables is easily computed: simply square the correlation coefficient. What you get when you do this is sometimes startling. For example, let's say that students' college entrance exam scores on the SAT are correlated with their first semester grade point average (GPA) in college, and we find that the correlation coefficient has a value of 0.70. That's a strong correlation, which means these two variables strongly relate to one another. But, how good a predictor of college GPA is the SAT test score? To determine this, we square 0.70 and get (0.70 x 0.70 =) 0.49. This means that 49 percent of the variance in college GPA scores can be explained by a person's scores on the SAT entrance exam. So, what explains the other 51 percent of the variance in GPA scores? It is other variables. The hard part is identifying what those variables are. This is why there are no really good bivariate prediction models in the social sciences. Human subjects are just too complex to be predicted in such simple ways. This is the foundation of prediction studies -- the search for sets of variables that explain as much variance in one variable as possible. Here's a little terminology you might encounter in your study of correlational research designs (especially prediction studies). The independent variables are frequently called predictor variables, and the dependent variable is usually called the criterion variable. In order to do a prediction study, a researcher must, first, do a relationship study on all the variables he/she believes are involved in the prediction model. Evaluating Correlational Research StudiesWhat should you look for when evaluating a correlational research study? First of all, look for the common things we've been evaluating in all previous studies: sampling technique; existence of a valid research hypothesis, objective, or questions; and the validity and reliability of appropriate measures used to collect data. There is one additional thing to look for that doesn't fall into any of those categories. It relates to the alpha error level we discussed in Week 2. Recall that alpha error is the level of error the researcher is willing to accept or tolerate and still remain confident that the results of the study are true. Well, every time a researcher repeats the same statistical test on the same set of data, the alpha error increases. This is extremely important in correlational research studies, because computers are capable of correlating dozens, hundreds, even thousands of variables in a very short time. For example, let's say a researcher wants to determine if significant relationships exist among five variables (A, B, C, D, and E). The intercorrelations of these five variables is usually displayed in the form of a matrix with the same number of rows and columns as the number of variables being correlated.
* p < .05 Notice the "-" signs down the diagonal (called the main diagonal) of the matrix. These are usually ignored because they're perfect correlations of each variable with itself. Also note that the correlations above and to the right of the main diagonal (called the upper triangular matrix) is a mirror image of the correlations below and left of the main diagonal (called the lower triangular matrix). Often, either the upper or lower triangular matrix is shown in research reports to reduce the amount of confusion in the table. The total number of correlation coefficients in this matrix (including those along the diagonal) is 5 x 5 = 25 intercorrelations. What we have here is the same statistical test (correlation coefficient) repeated on the same data set (same set of 5 variables) 25 times. If there had been, say, only two statistically significant coefficients. There would be very little reason for excitement since at least one of them could have occurred by chance. When evaluating correlational research studies, try to determine the number of potential chance correlations, as we did above, so you will have a better feel for the true significance of the results reported by the researcher. (Burnout and Counselor-Practitioner Expectations of Supervision)
If you have any questions concerning this evaluation (if you found things I didn't discuss here, or if you don't understand something I've discussed here), talk with other members of the course to see if you can resolve the issues with them. If not, discuss your questions with the instructor in class or via email.
|
Correlation research - Psychologos
Correlation analysis is a method of processing statistical data, which consists in studying the coefficients (correlations) between variables. In this case, the correlation coefficients between one pair or multiple pairs of features are compared to establish statistical relationships between them.
In this case, the correlation coefficients between one pair or multiple pairs of features are compared to establish statistical relationships between them.
General information
The goal of correlation analysis is to provide some information about one variable with the help of another variable. In cases where it is possible to achieve the goal, the variables are said to be correlate . In the most general form, the adoption of the hypothesis of the presence of a correlation means that a change in the value of variable A will occur simultaneously with a proportional change in the value of B: if both variables increase, then the correlation is positive , if one variable grows and the second decreases the correlation is negative .
Restrictions
1. Application is possible if there are enough cases to study: for a particular type of correlation coefficient is from 25 to 100 pairs of observations.
2. The second limitation follows from the hypothesis of correlation analysis (see above), which includes a linear dependence of variables . In many cases, when it is reliably known that the dependence exists, the correlation analysis may not give results simply because the dependence is not linear (expressed, for example, as a parabola).
The second limitation follows from the hypothesis of correlation analysis (see above), which includes a linear dependence of variables . In many cases, when it is reliably known that the dependence exists, the correlation analysis may not give results simply because the dependence is not linear (expressed, for example, as a parabola).
3. By itself, the fact of correlation does not give grounds to assert which of the variables precedes or is the cause of changes, or that the variables are generally causally related to each other, for example, due to the action of a third factor. (see Spurious Correlation, below).
Scope
This method of processing statistical data is very popular in the social sciences (especially in psychology), although the scope of correlation coefficients is extensive: quality control of industrial products, metallurgy, agrochemistry, and so on.
The popularity of the method is due to two points: the correlation coefficients are relatively easy to calculate, their application does not require special mathematical training. Combined with the ease of interpretation, the ease of application of the coefficient has led to its widespread use in the field of statistical data analysis.
Combined with the ease of interpretation, the ease of application of the coefficient has led to its widespread use in the field of statistical data analysis.
False correlation
Often, the alluring simplicity of a correlation study encourages the researcher to draw false intuitive conclusions about the presence of a causal relationship between pairs of traits, while correlation coefficients establish only statistical relationships.
This is illustrated by a well-known anecdote: if you go outside and measure the size of shoes and IQ of 1000 random passers-by, a statistically significant correlation will be found between them. However, this does not mean that foot size affects intelligence, since factors such as gender and age of study participants most likely influenced the presence of this relationship.
In the modern quantitative methodology of the social sciences, there has actually been a rejection of attempts to establish causal relationships between observed variables by empirical methods. Therefore, when researchers in the social sciences talk about establishing relationships between the variables under study, they imply either a general theoretical assumption or a statistical dependence.
Therefore, when researchers in the social sciences talk about establishing relationships between the variables under study, they imply either a general theoretical assumption or a statistical dependence.
3. Experimental and correlation studies
IN social psychology distinguish three main types of research: descriptive, correlation and experimental. The purpose of descriptive research is to give answer to the question whether this phenomenon. To this end, the researcher seeks to provide a detailed description of or some other phenomenon. To answer this question can he use pretty a wide range of methods for collecting information: observation, analysis of documents, surveys, tests. However, descriptive studies are superficial and reveal the causes of the phenomena.
More deep penetration into essence of occurring phenomena gives correlation study. Target correlation study — determine if there is any relationship (correlation) between those or other variables. correlation research can be carried out on a large amount of data. High correlation efficiency research is that it carried out in a real reality, where the researcher may consider the manifestation of such social factors like race, gender, social status, etc., which impossible to manipulate in the laboratory. When conducting a correlation research also uses a large set of methods: observation, analysis documents, polls. Link detection between some of the variables be a necessary step in establishing causes of one or the other phenomena, but based on information about correlations are not yet accurate. conclusions about causal relationships. It is possible in this situation And other variables. Therefore, the correlation research gives inaccurate, non-rigorous, ambivalent result.
correlation research can be carried out on a large amount of data. High correlation efficiency research is that it carried out in a real reality, where the researcher may consider the manifestation of such social factors like race, gender, social status, etc., which impossible to manipulate in the laboratory. When conducting a correlation research also uses a large set of methods: observation, analysis documents, polls. Link detection between some of the variables be a necessary step in establishing causes of one or the other phenomena, but based on information about correlations are not yet accurate. conclusions about causal relationships. It is possible in this situation And other variables. Therefore, the correlation research gives inaccurate, non-rigorous, ambivalent result.
Counts, which is the most precise, unambiguous result about cause and effect connections in socio-psychological phenomena gives experimental study. experimental research is more reliable method of establishing causal connections in socio-psychological phenomena compared to descriptive or correlational types of research.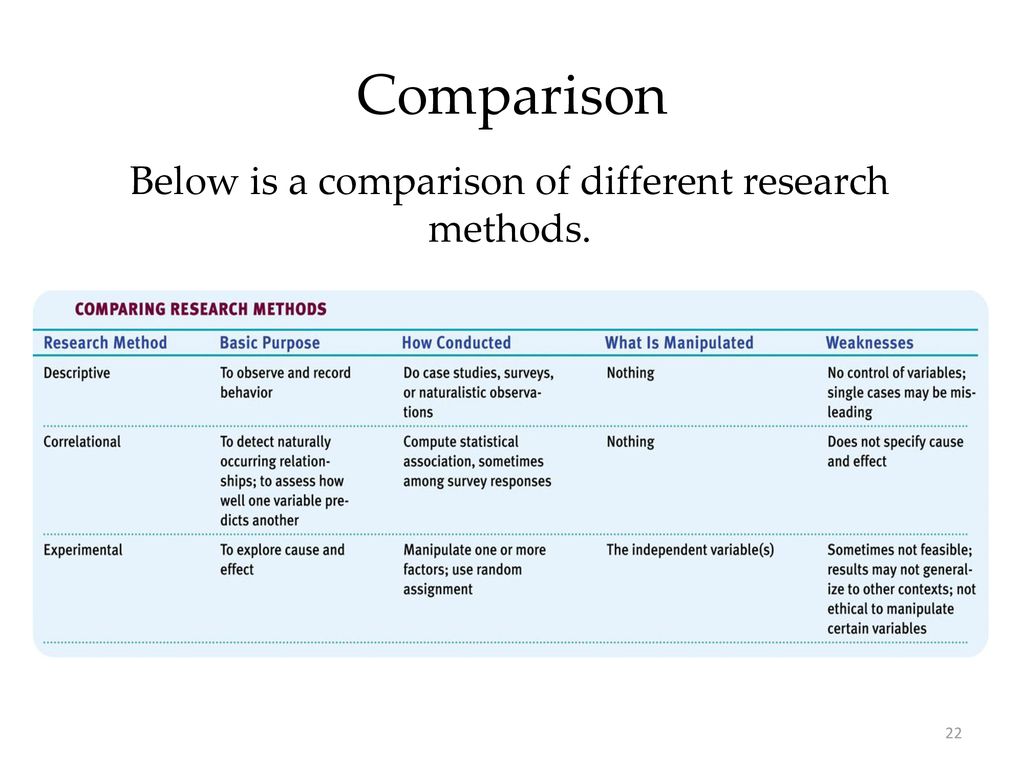 But being a more reliable method, it does not is absolute. In socio-psychological literature, in addition to those mentioned above. shortcomings of the laboratory experiment There are a number of other important considerations questioning the credibility causal inferences from experimental results. These doubts associated, according to J. Gergen, with cultural conditionality of social events. Gergen emphasizes that "only very few stimuli with their independent actions are capable of causing the predicted social behavior". Noting certain problems in explanation causal relationships obtained through experiment, even the most harsh critics don't advocate abolition of the experimental type research. They believe that in certain boundaries this type research plays a big positive role. Experiments are useful for comprehension deep nature of a social phenomenon, they can reinforce the theory, reveal the conditions under which she predictive value. However, on experiments cannot be done conclusions about any patterns in social processes or principles social behavior that preserves validity over time.
But being a more reliable method, it does not is absolute. In socio-psychological literature, in addition to those mentioned above. shortcomings of the laboratory experiment There are a number of other important considerations questioning the credibility causal inferences from experimental results. These doubts associated, according to J. Gergen, with cultural conditionality of social events. Gergen emphasizes that "only very few stimuli with their independent actions are capable of causing the predicted social behavior". Noting certain problems in explanation causal relationships obtained through experiment, even the most harsh critics don't advocate abolition of the experimental type research. They believe that in certain boundaries this type research plays a big positive role. Experiments are useful for comprehension deep nature of a social phenomenon, they can reinforce the theory, reveal the conditions under which she predictive value. However, on experiments cannot be done conclusions about any patterns in social processes or principles social behavior that preserves validity over time.
 ..)
..) Don't believe me? Can the lights in a room go off without moving the light switch? Can you move a light switch to "on" and lights don't come on? The answer to both questions is, of course, yes. The light switch does NOT cause the lights to go on or off -- it controls the flow of electricity, and electricity is what makes the lights go on or off. So, there is a relationship between the light switch and the lights, but not a cause-and-effect relationship. But what is someone didn't know about electricity? They would see someone moving the light switch and the lights going on and off. That person would conclude that the light switch caused the lights to go on and off. And, of course, they would be wrong. So how can you tell if something that relates to something else actually causes it to happen? You can't without doing a special, controlled study. To sum this up simply,
statisticians have a saying: "correlation does not imply causation", which means that just because two variables correlate with each other does not necessarily mean that one causes the other to occur.
Don't believe me? Can the lights in a room go off without moving the light switch? Can you move a light switch to "on" and lights don't come on? The answer to both questions is, of course, yes. The light switch does NOT cause the lights to go on or off -- it controls the flow of electricity, and electricity is what makes the lights go on or off. So, there is a relationship between the light switch and the lights, but not a cause-and-effect relationship. But what is someone didn't know about electricity? They would see someone moving the light switch and the lights going on and off. That person would conclude that the light switch caused the lights to go on and off. And, of course, they would be wrong. So how can you tell if something that relates to something else actually causes it to happen? You can't without doing a special, controlled study. To sum this up simply,
statisticians have a saying: "correlation does not imply causation", which means that just because two variables correlate with each other does not necessarily mean that one causes the other to occur.
 You will also notice that correlational research studies do NOT form groups. They are like descriptive research designs in this respect. So, if you look in the Methodology section of the research report and find that no groups are formed, then you know it cannot be causal-comparative research. It must be either descriptive or correlational. The difference between these two designs can really only be found in the purpose statement.
You will also notice that correlational research studies do NOT form groups. They are like descriptive research designs in this respect. So, if you look in the Methodology section of the research report and find that no groups are formed, then you know it cannot be causal-comparative research. It must be either descriptive or correlational. The difference between these two designs can really only be found in the purpose statement.
 75 are of equal strength. Note: positive correlation coefficients are usually shown without any sign in front of the number.
75 are of equal strength. Note: positive correlation coefficients are usually shown without any sign in front of the number.
 You could check virtually any elementary statistics text and find some rule-of-thumb regarding what constitutes strong and weak correlations. Here's a typical range of values that'll work for our needs:
You could check virtually any elementary statistics text and find some rule-of-thumb regarding what constitutes strong and weak correlations. Here's a typical range of values that'll work for our needs:
 That is, it's quite possible for a correlation coefficient of 0.1 to be statistically significant. This would mean that the two variables have very little relationship to one another, and that result is most probably NOT a chance occurrence. On the other hand, a correlation coefficient of 0.95 might not be statistically significant. This would mean that although in this study the relationship between the two variables was very strong, indeed, it most likely occurred by chance in this particular study, and would not likely occur again in another sample from the same population. So, do NOTassume that large coeffients are automatically statistically significant or that small coefficients are not. There is no connection between the size of the correlation coefficient and whether or not it's statistically significant. Whether a correlational value is statistically significant depends largely on the size of the sample. Just concetrate on the "p" value associated with each correlation coefficient, and if it is less than the alpha level set by the researcher, then the coefficient will be statistically significant, regardless of its numerical value.
That is, it's quite possible for a correlation coefficient of 0.1 to be statistically significant. This would mean that the two variables have very little relationship to one another, and that result is most probably NOT a chance occurrence. On the other hand, a correlation coefficient of 0.95 might not be statistically significant. This would mean that although in this study the relationship between the two variables was very strong, indeed, it most likely occurred by chance in this particular study, and would not likely occur again in another sample from the same population. So, do NOTassume that large coeffients are automatically statistically significant or that small coefficients are not. There is no connection between the size of the correlation coefficient and whether or not it's statistically significant. Whether a correlational value is statistically significant depends largely on the size of the sample. Just concetrate on the "p" value associated with each correlation coefficient, and if it is less than the alpha level set by the researcher, then the coefficient will be statistically significant, regardless of its numerical value.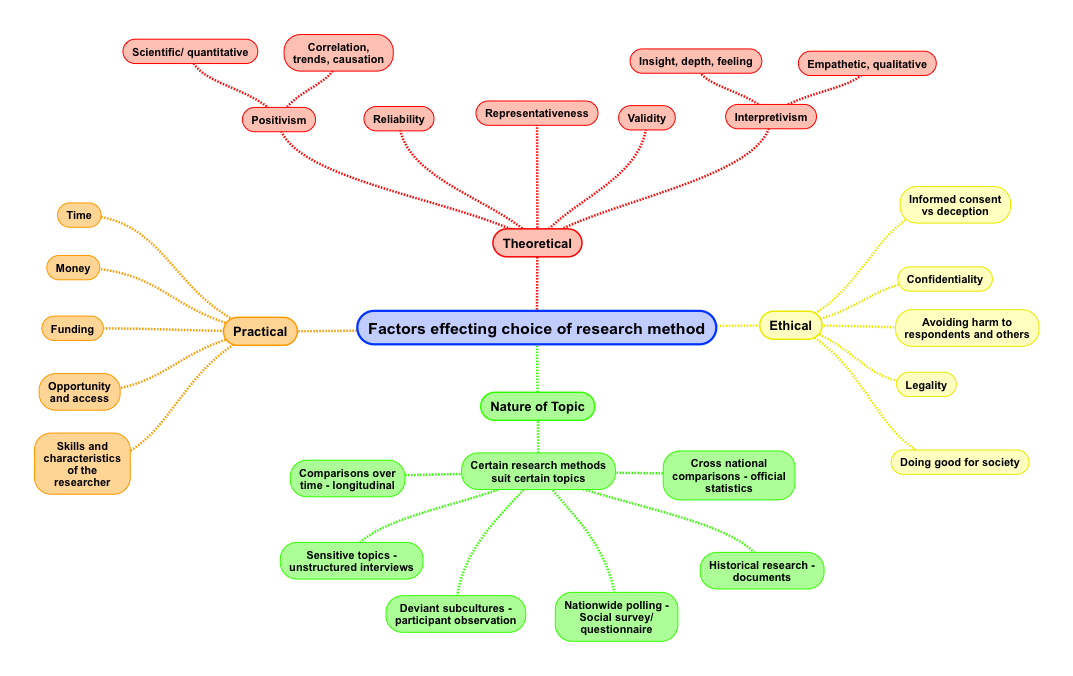
 Take a look for a moment at the different forms the variables can take, and that there is a different statistic for each data type. The majority of the statistics in the table are nonparametric and are, by their nature, rather weak. Certainly weaker than their parametric counterparts. They are so weak, in fact, that their limited power needs to be focused around narrow ranges to be effective. For example, look at the rho and tau coefficients. They are both used when the variables being correlated are in the form of ranks. But tau is preferred when the sample size is less than 10, while rho is preferred when the sample size is greater than 10 and less than 30.
Take a look for a moment at the different forms the variables can take, and that there is a different statistic for each data type. The majority of the statistics in the table are nonparametric and are, by their nature, rather weak. Certainly weaker than their parametric counterparts. They are so weak, in fact, that their limited power needs to be focused around narrow ranges to be effective. For example, look at the rho and tau coefficients. They are both used when the variables being correlated are in the form of ranks. But tau is preferred when the sample size is less than 10, while rho is preferred when the sample size is greater than 10 and less than 30.
 Actually, both of these are special types of categorical data. Dichotomies have only two possibilities -- so, only two categories. A true dichotomy is naturally occurring (not researcher-made) like gender (male and female). An artificial dichotomy is arbitrarily determined (usually by some kind of cut-off point) like a pass-fail point on a test, or rich-poor (someone arbitrarily determines the dividing line), etc. Get the idea?
Actually, both of these are special types of categorical data. Dichotomies have only two possibilities -- so, only two categories. A true dichotomy is naturally occurring (not researcher-made) like gender (male and female). An artificial dichotomy is arbitrarily determined (usually by some kind of cut-off point) like a pass-fail point on a test, or rich-poor (someone arbitrarily determines the dividing line), etc. Get the idea?
 " Understand? Good (I hope you said yes!) Let's try another example. Say you wanted to see if there was a relationship between gender and academic performance in high school (again, measured by an academic achievement test). What would be the most appropriate statistic to use? Check Table
12.3 (pg. 273) in the text, then check your answer here. Did you get it right? If not, talk with your classmates or with the instructor.
" Understand? Good (I hope you said yes!) Let's try another example. Say you wanted to see if there was a relationship between gender and academic performance in high school (again, measured by an academic achievement test). What would be the most appropriate statistic to use? Check Table
12.3 (pg. 273) in the text, then check your answer here. Did you get it right? If not, talk with your classmates or with the instructor.
 Now what?
Now what?
 Just because one thing can predict the occurrence of something else does not necessarily mean that one causes the other.
Just because one thing can predict the occurrence of something else does not necessarily mean that one causes the other.
 When you think about it, that's a pretty poor predictor. I could flip an honest coin and do a better prediction job than that!
When you think about it, that's a pretty poor predictor. I could flip an honest coin and do a better prediction job than that!
 So, the first part of the study is to identify relationships between variables of interest. Then, the second part is to use those relationships (coefficients) to create the model. We won't go into the details of creating the model, because it's far too detailed for this course. It's enough to draw your attention to the multivariate correlation techniques in your text in Table
12.4 on page 274. Each of these techniques provides a means of developing a prediction model based on correlation coefficients computed from a set of variables. The coefficients themselves are computed using the bivariate techniques listed in Table
12.3 in your text.
So, the first part of the study is to identify relationships between variables of interest. Then, the second part is to use those relationships (coefficients) to create the model. We won't go into the details of creating the model, because it's far too detailed for this course. It's enough to draw your attention to the multivariate correlation techniques in your text in Table
12.4 on page 274. Each of these techniques provides a means of developing a prediction model based on correlation coefficients computed from a set of variables. The coefficients themselves are computed using the bivariate techniques listed in Table
12.3 in your text.
 You should also pay attention to whether the researcher is using appropriate correlational statistical tests.
You should also pay attention to whether the researcher is using appropriate correlational statistical tests.
 In our example, that would be a "5 by 5" matrix that might look like this:
In our example, that would be a "5 by 5" matrix that might look like this:
 43
43 Now recall our discussion of the alpha error level (.05). This is the amount of error we are willing to tolerate and still be confident that the results are true. Well, given this error level, we can expect some of these correlation coefficients to be statistically significant -- purely by chance. How many and which ones will they be. We cannot know precisely which coefficients will show up as falsely statistically significant. But, we can estimate how many there will be. We can do this by simply multiplying the total number of intercorrelations by the alpha error level for the study, and rounding off the result. In our current example, we should expect 1 (25 x .05 = 1.25 = 1 (rounded)) of these 25 coefficients to be statistically significant by chance alone. A look at the correlation matrix above shows that 6 coefficients are statistically significant at the .05 level. This is much greater than the number that would be expected to occur by chance given the number of variables being correlated.
Now recall our discussion of the alpha error level (.05). This is the amount of error we are willing to tolerate and still be confident that the results are true. Well, given this error level, we can expect some of these correlation coefficients to be statistically significant -- purely by chance. How many and which ones will they be. We cannot know precisely which coefficients will show up as falsely statistically significant. But, we can estimate how many there will be. We can do this by simply multiplying the total number of intercorrelations by the alpha error level for the study, and rounding off the result. In our current example, we should expect 1 (25 x .05 = 1.25 = 1 (rounded)) of these 25 coefficients to be statistically significant by chance alone. A look at the correlation matrix above shows that 6 coefficients are statistically significant at the .05 level. This is much greater than the number that would be expected to occur by chance given the number of variables being correlated. So, these correlations are more than just chance occurrences.
So, these correlations are more than just chance occurrences.


 That means there are 81 possible intercorrelations (9 x 9). Using an alpha error level of .05 (which is OK because we weren't told what the alpha level was), the possible number of chance statistically significant correlations is 4 (81 x .05). How many coefficients actually turned out to be statistically significant? Counting all the correlations with asterisks by them shows 27. Since this is just for the lower triangular matrix, we would have to double this number to get the total for the whole matrix. That would be 54 statistically significant correlations (actual). Comparing this number to the 4 expected by chance leads us to conclude that there is reason for excitement about the significant relationships found between supervision variables in this study.
That means there are 81 possible intercorrelations (9 x 9). Using an alpha error level of .05 (which is OK because we weren't told what the alpha level was), the possible number of chance statistically significant correlations is 4 (81 x .05). How many coefficients actually turned out to be statistically significant? Counting all the correlations with asterisks by them shows 27. Since this is just for the lower triangular matrix, we would have to double this number to get the total for the whole matrix. That would be 54 statistically significant correlations (actual). Comparing this number to the 4 expected by chance leads us to conclude that there is reason for excitement about the significant relationships found between supervision variables in this study.

 Don't look at the answers on the second page until you have answered
all the questions yourself. Then compare your answers with those provided in
the problem. If you have questions or don't agree with or understand the
answers provided, E-mail me and let's discuss it.
Don't look at the answers on the second page until you have answered
all the questions yourself. Then compare your answers with those provided in
the problem. If you have questions or don't agree with or understand the
answers provided, E-mail me and let's discuss it.