Acting on impulse

Acting on Impulse | Psychology Today

We sometimes behave as if we had two selves. For instance, at the beginning of a meal, I might have decided not to have dessert (prefer health to indulgence), but when the time comes, I find that I have somehow changed my mind (prefer indulgence to health). However, in my own calm and reflective mind, I place more importance on health than the desert. There appears to be a gap between what we prefer to do and what we end up doing.

An important idea in behavioral economics is that our behavior seems to be controlled by a narrow-minded impulse that cares about immediate gratification and a farsighted thinking mind that is concerned with long-term satisfaction. When we are calm, the deliberative mind guides slow rational thinking and choices. This is the self that we are most aware of and prefer to present to the public.

The thinking mind is typically effortful. In contrast, the impulsive mind acts spontaneously without consideration for the broader consequences of the action. The everyday snap judgments (jumping to conclusions or reacting defensively) are made by the impulsive mind without processing information.

This important insight about the human mind explains why we are conflicted, inconsistent, and why we do foolish things. In these moments we often use our deliberative mind to justify or rationalize our behaviors (blaming others or denying). The inconsistencies in the mind give rise to self-control problems. The essence of the self-control problem is mainly about the conflict between two selves (e.g., one who wants to be thin and the other who wants to eat). A self-control problem implies that individuals are acting against their own better judgment of what is in their long-term interest.

The choice of an impulsive individual is highly influenced by external stimuli, pressures, and demands. For example, seeing and smelling fresh-baked cookies make one reach out before realizing one is on a diet. We then ask: “What was I thinking?” Sadly, the answer is: Not too much thinking was involved. Yet we might be unaware that our environment influences our behavior because stimuli can activate goals and cravings. This explains why it is easier to change our environment than to change our habits. Change the environment and then let the new cues do the work.

Strong emotions (anger and jealousy) can provoke knee-jerk reactions that may sometimes be difficult to reverse. For instance, angry decision-makers typically process information in distorted ways, fail to consider alternative options before acting. Anger triggers optimism about oneself. It triggers a bias toward seeing the self as powerful and capable. Anger is often a mask for helplessness, and it is a way of reasserting control and self-respect.

Emotions are relatively transient. What comes up often comes down. A typical emotional response involves a quick rise lasting for a few minutes and then followed by relatively slow decay. For example, anger usually lasts for more than a few minutes, but rarely more than a few hours. But people tend to mispredict the short duration of emotional experience.

However, we are not destined to grab immediate rewards we will later regret. There are ways that individuals can reduce their shortsighted behaviors. A well-cultivated self-awareness is a key to preventing acting impulsively. It helps us to observe our two selves in real-time and make choices based on our long-term goals. In the words of noble laureate Daniel Kahneman, life seems to consist of the struggle between short-sighted self and long-sighted self, and to balance these two is an art.

Source: Josethestoryteller/Pixabay

Impulsive Behavior: Symptoms, Causes, and Treatment

An impulsive behavior is when you act quickly with no thought to the consequences. There’s nothing on your mind beyond that exact moment.

We all engage in impulsive behavior from time to time, especially when we’re young. As we mature, we learn to control our impulses for the most part. It’s not necessarily part of a disorder.

Frequent impulsive behavior can be associated with certain mental health conditions.

By itself, impulsive behavior is not a disorder. Anyone can act on impulse once in a while.

Sometimes, impulsive behavior is part of an impulse control disorder or other mental health disorder. This may be the case when:

there’s a pattern of impulsive behavior
you’re unable to gain control over impulses
there are other signs and symptoms of mental illness

Acting on impulse is spontaneous. There’s no consideration to how it could affect others. There’s no wondering how you’ll feel about it later. It’s just about the here and now.

Examples of this include:

bingeing: overindulging in things like shopping, gambling, and eating
destruction of property: destroying your own or someone else’s things in a moment of anger
escalating problems: taking minor situations and making them more urgent and important than necessary
frequent outbursts: losing your cool far too often, even when it’s clearly uncalled for
lots of starting over: abruptly joining and quitting groups or wiping the slate clean in search of a fresh start
oversharing: talking without thinking and sharing intimate details
physical violence: overreacting by getting physical in the spur of the moment
higher risk sex: engaging in sex without a condom or other barrier method, especially with a person whose STI status is unknown
self-harm: hurting yourself in the heat of anger, sadness, or disappointment

Young children are often impulsive. That’s because they don’t yet realize how their own behavior can affect others. They may not understand that their actions have consequences beyond their immediate wants.

Some examples of this are:

ignoring danger: running into the street without checking traffic or jumping into a pool even though they can’t swim
interrupting: frequently butting into conversations
getting physical: pushing another child or throwing something when upset
grabbing: Taking what they want rather than asking or waiting for a turn
getting vocal: screaming or yelling in frustration

How we make decisions is a complex process. The cause of being impulsive may not always be evident.

People may also indulge in risky behavior for reasons other than impulsivity. It’s also not uncommon to see impulsiveness in young children who haven’t developed self-control.

Studies show that impulsivity may have something to do with the prefrontal lobe. Other research suggests an association between impulsivity and brain connectivity.

Researchers have a long way to go to fully understand the links between impulsivity and:

personality
brain connectivity
brain function

Physical conditions, such as brain lesions and stroke, can also lead to symptoms such as impulsive behavior.

Anyone can become frequently impulsive, but it can sometimes be a sign of an underlying disorder.

The following are some disorders that may lead to impulsivity. The exact causes for these disorders are unknown. They may develop due to a combination of factors that include:

genetics
environment
brain function
brain injury
physical changes in the brain
childhood trauma

Borderline personality disorder

Borderline personality disorder is a mental health condition involving emotional instability. Symptoms include:

impulsivity
poor self-image
dangerous behaviors
self-harm

Bipolar disorder

Bipolar disorder is a mental health condition marked by extreme shifts in mood, often mania or depression.

In a manic episode, someone may have the symptom of impulsive behavior. Other symptoms include:

high energy
agitation
racing thoughts and talkativeness
euphoria
less need for sleep
poor decision-making

Attention deficit hyperactivity disorder (ADHD)

People with ADHD can find it hard to pay attention and control impulsive behavior. Symptoms can include:

restlessness
forgetfulness
interrupting others
trouble focusing or concentrating

Substance use

Certain substances, such as alcohol, can break down inhibitions. This can lead to impulsive behavior.

On the other hand, impulsivity may contribute to the development of substance use disorders. It may not be possible to determine which came first.

Antisocial personality disorder

Antisocial personality disorder involves impulsive and manipulative behavior. Other symptoms are:

quick to anger
arrogance
lying
aggressiveness
a lack of remorse

Intermittent explosive disorder

In intermittent explosive disorder, a person experiences frequent episodes of impulsive or aggressive behavior. Examples of this are:

temper tantrums
physical violence
road rage

Kleptomania

Kleptomania is a rare condition in which you can’t resist the compulsion to steal. People with kleptomania tend to have coexisting mental health disorders. These can include anxiety and depression.

Pyromania

Pyromania is a rare mental health disorder — a type of impulse control disorder — in which you can’t control the impulse to set fires.

Trichotillomania

Trichotillomania is another rare condition. It involves a powerful desire to pull out your own hair.

This condition is a type of obsessive-compulsive disorder, though it was formerly classified as an impulse control disorder.

Brain injury or stroke

Brain injury or stroke can lead to changes in behavior. This includes:

impulsiveness
poor judgement
short attention span

Even if you don’t have a diagnosis of a mental health condition, frequent impulsive behavior is something you should address.

Impulsive behavior can lead to other inappropriate behaviors with potentially serious consequences. Research shows a relationship between impulsivity and:

suicide in people who have borderline personality disorder
drug misuse in those who use multiple drugs
manic episodes
depressive episodes

Other research shows a link between impulsiveness and violent behavior.

If you or your child frequently behave on impulse, see a doctor. You can start with a primary care physician or pediatrician. If necessary, they can refer you to a mental health specialist.

How to approach this behavior depends on the cause. In many cases, the person is not at fault. They may not have the ability to change.

When it’s your child, you can:

make them aware of their impulsivity and how it affects them later
explore alternative behaviors by role-playing
teach and practice patience

You can deal with your own impulsive tendencies by:

mentally walking through potential scenarios and practicing how to stop and think before acting
dealing directly with your usual impulsiveness by making it harder to binge, splurge, or dive headlong into things

If you feel that you can’t gain control on your own, a healthcare professional can provide helpful resources.

Everyone behaves impulsively sometimes. Most of the time, we can work to limit those behaviors on our own.

Sometimes, impulsive behavior is part of an impulse control disorder or other type of mental health condition. These disorders can be treated.

If you have major problems due to impulsive behavior, help is available. Take the first step and see a doctor.

Chapter 5. The law of conservation of momentum

The momentum of a body is a vector quantity equal to the product of the mass of the body and its speed

(5.1)

The impulse of a system of bodies is the vector sum of the impulses of all bodies included in this system. There are two laws associated with momentum that can be used to find the velocities of bodies.

Newton's second law can be written through the change in the momentum of the body. Indeed, since the acceleration of the body is

(5. 2)

where are the forces acting on this body from other bodies. Formula (5.2) is usually called Newton's second law in impulsive form.

For a system of bodies that interact only with each other, but not with other bodies (such a system of bodies is called closed), the momentum conservation law is satisfied. This law states that the momentum vector of such a system of bodies does not change

over time, although the impulses of the individual bodies of the system may change. Let us consider the application of these definitions and laws to the solution of problems.

When solving problem 5.1.1 , it should be remembered that momentum is a vector quantity, and therefore the momentum of a body changes when it rotates around a circle at a constant speed. In particular, the magnitude of the change in the momentum of the body for half the period of movement along the circle is equal to (see the figure, the subtraction of vectors is performed on the right side of the figure). Therefore, the correct answer in the problem is 2 .

The momentum of the system of bodies given in problem 5.1.2 is found using the vector addition of the momenta of the individual bodies included in the system (see figure). Using the Pythagorean theorem, we find the momentum of the system (answer 4 ).

In problem 5.1.3 it is convenient to use Newton's second law in the impulse form (5.2). Since the force acting on the body is constant, the law (5.2) can be applied not only to an infinitely small, but also to a finite time interval. From law (5.2) we have

where and are the initial and final impulses of the body, is the force acting on the body, is the duration of the force. Since, according to the condition, the vectors of the initial momentum and force are directed oppositely, we find by projecting Newton's second law onto the direction of the initial momentum kg • m/s (answer 2 ).

With the help of Newton's second law in impulsive form it is also convenient to solve the following problem 5.1.4. Applying this law to the hammer (it must be taken into account that after the blow the hammer stopped, and, therefore, ), we find the average force acting on it from the side of the nail, which is equal to the force acting from the side of the hammer on the nail

(answer 2 ).

Problem 5.1.5 is very simple. However, schoolchildren do it poorly (perhaps precisely because of its simplicity). Since the momentum of a closed system is conserved, then for the system of carts at any moment of time it will be the same as at the initial moment, regardless of the nature of the collision (whether they were mated or not, scattered, etc.). And since at the initial moment the momentum of the system is equal to 1 kg • m/s, then it will be the same in the future (answer 1 ).

Applying the law of conservation of momentum to the collision of carts of of task 5.1.6 , we obtain , where is the total mask of carts, is their speed after the collision. From here we find that (answer 3 ).

The law of conservation of momentum for the "bar-bullet" system from problem 5.1.7 gives

where is the speed of the bar with the bullet stuck in it. From here we find that (answer 1 ).

In problem 5.1.8 the collision of bodies is considered, which then stick together. If the bodies stop after the collision, then the momentum of this system of bodies after the collision is equal to zero. Consequently, the momentum of the system of bodies before the collision must also be equal to zero. Therefore, before the collision, the equality must be satisfied , where , and , are the masses and velocities of the bodies before the collision. From here we find m / s (answer 3 ).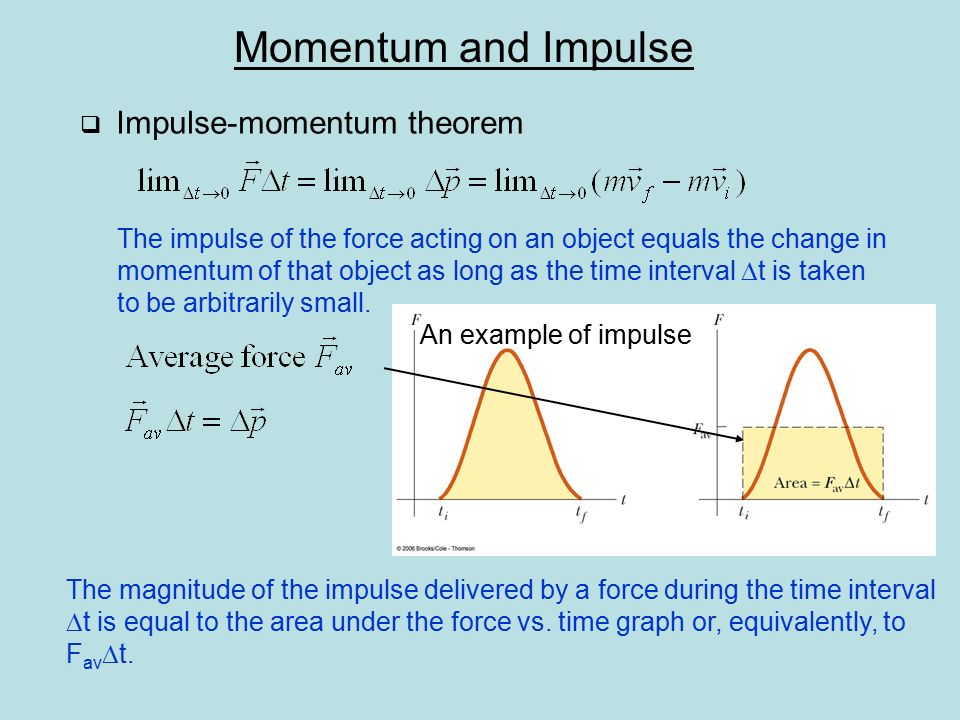

The momentum conservation law for the bullet-bar body system from problem 5.1.9 has the form

where is the speed of the bar after it has been pierced by the bullet. Therefore (answer 1 ).

From the momentum conservation law in problem 5.1.10

where and are the momenta of the first body before and after the collision, is the momentum of the second body after the collision, we find

which means that the velocity vector of the second body after the collision is directed as shown in the figure 3 in the problem statement.

Obviously, the speed of the trolley after the "accurate" dropping of the body (ie with zero speed relative to the trolley) does not change ( task 5.2.1 ). Indeed, it follows from the law of conservation of momentum that the speed of the cart will change if the speed of the body also changes (so that the total momentum of the "cart-body" system does not change). In the case under consideration, the speed of the body does not change, so the speed of the cart does not change either.

The law of conservation of momentum for a person and a cart moving in the same direction ( task 5.2.2 ) has the form

from where we get the answer given in the condition of the problem 4 . Note that the rest of the data in the answer condition could be “discarded” immediately: in two of them, with the same masses of a person and a trolley, zero in the denominator is obtained (which is impossible), another answer gives zero for the speed at the same speeds of a person and a trolley (and the answer in this case, obviously, should give exactly this speed).

The momentum conservation law for the system of bodies "cart with sand - ball" from problem 5.2.3 has the form

where , and , are the masses and velocities of the cart and the ball before the collision, are the speed of the cart with the ball after the collision. Projecting the law of conservation of momentum onto the axis (see figure), we find

where is the projection of the vector onto the axis . It follows that the speed vector of the cart with the ball is directed against the axis and is equal in value to 0.1 m/s (answer 2 ).

Consider the momentum conservation law for a grenade ( problem 5.2.4 ) , where and are the masses of two fragments, and are their velocities after the explosion. Projecting this law onto the direction of motion of the grenade, we obtain

(1)

where is the projection of the velocity of the second fragment on this direction. It follows from formula (1) that the second fragment moves after the explosion opposite to the direction of the grenade before the explosion, if , since in this case the projection of the vector on the direction of the grenade before the explosion is negative (the answer is 2 ).

Problems 5.2.5 and 5.2.6 are set very similar to each other, but in the first of them the speed of a person relative to the ground is given, in the second - relative to the cart. And what speed should be used in the law of conservation of momentum? In fact, you can take speeds in any frame of reference, but it is important that all speeds are given in the same frame. And since the initial speed of the cart relative to the ground is known, it is convenient to set all speeds in this system. AT problem 5.2.5 we have in the reference system associated with the earth in projections on the axis directed along the speed of the cart

where is the speed of the cart after the collision. From here we find

(the correct answer is 1 ).

Law of conservation of momentum in problem 5.2.6

in which all speeds are given relative to the ground ( - the speed of a person relative to the ground), must be combined with the law of addition of speeds

where is the speed of a person relative to the ground, is the speed of the trolley. Substituting the law of addition of velocities into the law of conservation of momentum, we have

Projecting this vector law onto the direction of movement of the cart, we get

(the correct answer is 3 ). Note that the difference between the answers of this and the previous problems is reduced to the difference between their denominators.

In problem 5.2.7 it is necessary to consider the law of conservation of momentum in the case when the velocities of the bodies after the collision are not directed along one straight line. From the momentum conservation law for projectile

have

Location

(the correct answer is 3 ).

Since the projection of the momentum of the system of bodies in problem 5.2.8 on the axis (see figure) is equal to zero, after sticking the bodies will move along the axis . Therefore, from the projection of the law of conservation of momentum of the system on the axis

where is the speed of the bodies after the collision, we get (the answer is 3 ).

Since the momentum of the initial nucleus is equal to zero ( problem 5.2.9 ), the vector sum of the momenta of the fragment nuclei is also equal to zero. Therefore , where , and are the momenta of the first, second, and third fragments. By convention, the vectors and are directed perpendicular to each other. Therefore, the magnitude of the vector can be found using the Pythagorean theorem

From here we find the speed of the third fragment (the answer is 1 ).

In problem 5.2.10 , we first consider the movement of a body along the surface of the hill, when the body B is fixed and can only move together with the hill. According to the law of conservation of momentum, after the body slides to the left, the slide with the body will move to the right with a certain speed (see figure), and the greater the mass of the slide with the body compared to the mass of the body, the less speed the slide will acquire. Let us now consider the sliding of the body , but we will do it in the frame of reference associated with the slide. In it, the slide stands at the initial moment, and then after the body slides to the right, it will move to the left. If the slide acquired the same speed as in the first case, then in the reference frame associated with the earth, it would stop. It can be understood, however, that in the second case the slide will acquire greater speed. Indeed, in the first case, the body, when sliding, pushed the hill in the opposite direction along with the body, and the body pushed only one hill (i. e., a lighter body). Therefore, after successive slipping of two bodies (first , then ), the slide will move to the left (answer 1 ).

§3. Impulse of the system of material points. Theorem on the change in the momentum of a system of material points — ZFTSh, MIPT

Consider a system of material points with masses `m_1`, `m_2 ...`, moving in an arbitrary IFR with velocities `vecv_1`, `vecv_2 ...`. The impulse `vecP_sf"с"` of the system of material points is the vector sum of the impulses of the material points that make up the system: `vecP_sf"с" = vec p_1 + vec p_2 + ...`.

Let's find the speed `(Delta vec P_sf"s")/(Delta t)` of change in the momentum of the system of material points (we know the answer to this question for one material point). For example, consider a system of two material points. We will assume that the first material point is acted upon by the total force `vec F_1` external to the system of the body and the internal force `vec f_(12)` from the second body. In turn, the second material point is affected by bodies external to the system, the sum of these forces `vec F_2` and the internal force `vec f_(21)` from the first body. Then, taking into account Newton's second law, for each body we obtain

According to Newton's third law `vec f_(12) + vec f_(21) = vec (0)`, and we arrive at the theorem on the change in the momentum of the system of material points:

From the above proof it follows that Newton's third law can be formulated and as a requirement of conservation of momentum for a system of interacting bodies if there are no other external forces.

This is its deeper physical content.

According to Newton's third law, the required forces are related to the friction force `vec(R_1) = - vecF_("tr")` and the normal reaction force `vec R_2 = - vecN_("r")` acting on the wedge from the side of the support ( Fig. 7).

The forces `vec F_("tr")` and `vecN_("g")`, along with the forces of gravity, are external to the "wedge + bar" system and determine the rate of change of momentum of this system.

. To determine the rate of change of momentum `vec p` of the bar, let's turn to Newton's second law (Fig. 8):

`(Delta vec p)/(Delta t) = m vec g + vec N + vecf_("tr")`.

Turning to the projections of increments of the momentum of the bar and forces on the axes `Oy` and `Ox`, taking into account the relation `f_sf"tr" = mu N` we get:

`(Delta p_y)/(Delta t) = 0 = N - mg cos alpha`, `(Delta p_x)/(Delta t) = mg (sin alpha - mu cos alpha)`.

According to the theorem on the change in momentum of the "wedge + bar" system

vecF_("tr")`.

Passing in the last equality to the projections on the horizontal and vertical directions (Fig. 7), taking into account

Pc,x~=pxcosαP_{\mathrm c,\widetilde x}=p_x\cos\alpha

we get

Pc ,y~=-pxsinαP_{\mathrm c,\widetilde y}=-p_x\sin\alpha,

{\mathrm c,\widetilde x}}{\triangle t}=\dfrac{\triangle\left(p_x\;\cos\alpha\right)}{\triangle t}=mg\left(\sin\alpha- \mu\cos\alpha\right)\cos\alpha=F_\mathrm{tr},

∆Pc,y~∆t=∆-px sinα∆t=-mgsinα-μcosαsinα=-M+mg+Ng\dfrac{\triangle P_{c,\widetilde y}}{\triangle t}=\dfrac {\triangle\left(-p_x\;\sin\alpha\right)}{\triangle t}=-mg\left(\sin\alpha-\mu\cos\alpha\right)\sin\alpha=-\ left(M+m\right)g+N_\mathrm g.

Learn more